Lecture #10: Sorting & Aggregation Algorithms

참고자료: Youtube - F2023 #10 - Sorting & Aggregation Algorithms (CMU Intro to Database Systems)

Query Plan

SQL문을 실행하면, DBMS는 쿼리를 Compile하여 Query Plan으로 변환한다. Query Plan은 Operator(Relational Operator)로 구성된 Tree를 의미한다.

1
2
3
4

SELECT R.id, S.cdate
FROM R JOIN S
ON R.id = S.id
WHERE S.value > 100

위의 쿼리문을 실행하면, RDBMS는 쿼리를 아래의 Relational Algebra로 변환한다.

πR.id,S.cdate(R▷◁(σvalue>100(S))

또한 위의 Relational Algebra는 아래의 Tree 형태(Root Node가 1개인 DAG)로 표현이 가능하다. Tree의 각 Node는 Operator를 의미한다.

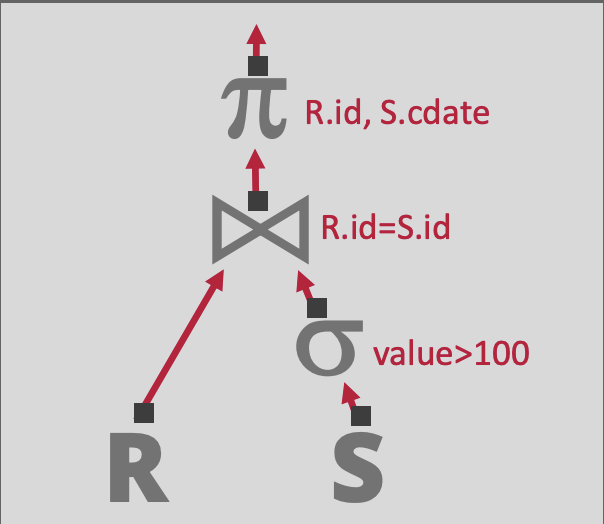
데이터는 Tree의 Leaf Node로부터 공급되며, Root Node로 흐르게 된다. Root Node의 결과가 곧 Query의 결과가 된다.

Disk-Oriented DBMS

Disk-Oriented DBMS라는 제목이지만, 분산 데이터베이스 혹은 데이터 처리 엔진에서도 동일한 이슈가 존재하며 유사한 방법으로 문제를 해결한다.

Relational Algebra의 Operator가 사용하는 알고리즘은 다음 사항들을 가정하고 설계해야 한다.

• 사용 가능한 메모리 용량을 넘어서는 데이터를 다룰 수 있어야 한다.
• 자주 사용되는 데이터에 빠르게 접근할 수 있도록 Buffer Pool 기반으로 동작할 수 있도록 설계해야 한다.
• 디스크 접근 시 Sequential I/O의 사용을 극대화 할 수 있도록 설계야해 한다.

Sorting

이전에 정의했든 Relational Model은 정렬되지 않은 집합(relation)에 기반한 모델이다. SQL에는 명시적 혹은 묵시적으로 정렬을 필요로 하는 연산이 존재하는데, 이를 위해 정렬의 구현이 필요하다. 정렬을 필요로 하는 경우는 다음과 같다.

• 쿼리에 ORDER BY 구문이 포함되어 있는 경우 - 명시적
• GROUP BY, JOIN, DISTINCT 등의 Operator를 사용하는 경우 - 묵시적

Aggregation의 경우 Hash 기반으로 구현할 수도 있지만, Sort 기반으로 구현할 수도 있다. 대부분의 경우 Hash 기반의 Aggregation이 사용되지만, 몇몇 경우는 Sort 기반의 Aggregation이 사용될 수 있다.

메모리 용량이 모든 데이터를 수용 가능한 경우, Quick Sort 등의 일반적인 In-Memory Sorting을 사용할 수 있다.

Python, Java 등에서는 실제 데이터에서 좀 더 잘 동작하는 TimSort를 기본 정렬 알고리즘으로 사용한다. TimSort는 Merge Sort와 Insertion Sort가 혼합된 정렬 알고리즘이다.

그러나 메모리에 모든 데이터를 로드할 수 없는 경우, DBMS는 필요한 경우 중간 데이터를 디스크에 쓸 수 있는(Sequential I/O를 중심으로) External Sorting을 사용해야 한다.

Top N Heap Sort

In-Memory Sorting의 예시로 제시하였다.

ORDER BY와 LIMIT이 함께 사용된 쿼리의 경우, RDBMS는 한 번의 스캔만으로 상위 N개의 Element들을 찾아낼 수 있다.

1
2
3
4

SELECT * FROM enrolled
ORDER BY sid
FETCH FIRST 4 ROWS
WITH TIES

위의 쿼리의 경우 sid를 기준으로 상위 4개의 ROW를 찾아내야 하는데, 이 연산에 가장 적합한 In-Memory Sorting Algorithm은 Heap Sort(= in-memory sorted Priority Queue)이다.

입력 데이터가 [3, 4, 6, 2, 9, 1, 4, 4, 8] 일 때, [3] -> [4, 3] -> [6, 4, 3] -> [6, 4, 3, 2] -> [4, 3, 2, 1] -> [4, 4, 3, 2, 1] -> [4, 4, 4, 3, 2, 1]의 순서로 상위 4개의 Element들을 골라낼 수 있다.

Heap 자료구조가 최대 값과 크기를 메모리에 유지하고 있을 수 있기 때문에, 새로운 Element를 삽입할지에 대한 여부를 즉시 판단할 수 있다.

External Merge Sort

메모리에 모든 데이터를 로드할 수 없는 경우, 일반적으로 사용되는 정렬 알고리즘이 External Merge Sort이다. External Merge Sort는 데이터를 작은 단위(RUN)로 분할하고, 각각의 RUN을 정렬한 뒤, 이를 큰 단위의 RUN으로 합치는 분할-정복 알고리즘이다.

• Sorting: 데이터를 메모리에 올릴 수 있을 정도의 크기로 분할(Chunking)하여, 각 분할된 데이터(Chunk) 단위로 정렬한다. 정렬된 데이터는 다시 Disk에 쓴다.
• Merge: 디스크에 써진 정렬된 Chunk를 합쳐 새로운 Chunk를 만들고, 이를 Disk에 쓴다.

SORTED RUN

RUN은 키-값 쌍의 리스트를 의미한다.

• 키: 정렬 순서를 결정하는 Attribute이다.
• 값: 정렬 순서와 관계 없는 Attribute의 집합이다.

값은 두가지 방식으로 표현 가능한데, Tuple(Early Materialization) 방식과 Record ID(Late Materialization) 방식이 존재한다.

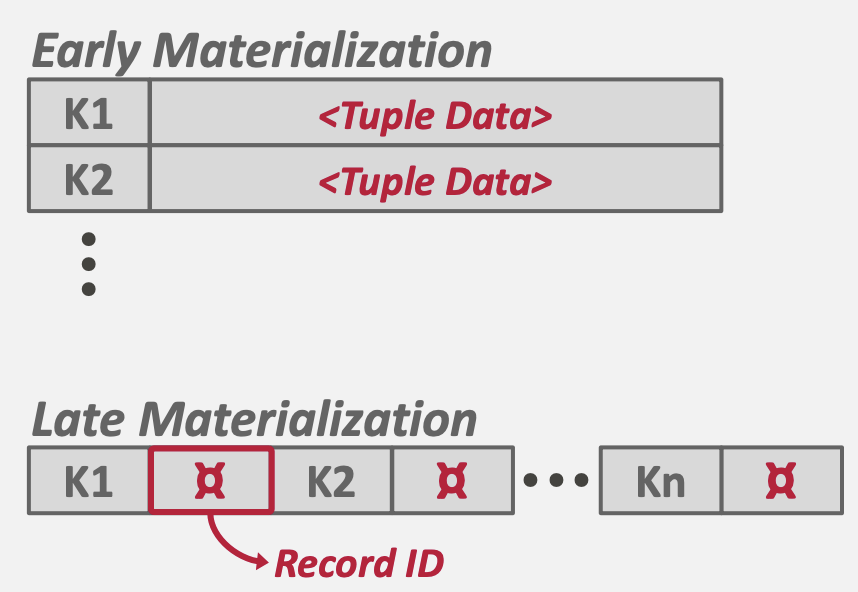
• Tuple 방식: 실제 데이터를 값으로 유지한다. 정렬 후 즉시 값에 접근이 가능하다.
• Record ID 방식: 데이터가 저장된 주소(메모리 혹은 디스크)를 값으로 유지한다. 정렬 후 값에 접근하기 위해 주소를 참조하여 실제 값을 읽어야 한다.

Tuple 방식은 보통 Row-Oriented RDBMS에서 많이 사용되고, Record ID 방식은 Column-Oriented RDBMS에서 많이 사용된다고 한다.

Row-Oriented RDBMS의 경우 대부분 Row 의 전체 값을 읽어야 하는 경우가 대다수이지만, Column-Oriented RDBMS의 경우 특정 컬럼만 읽는 경우가 다수이기 때문에 모든 데이터를 값으로 유지하는 것이 비효율적이다.

2-Way External Merge Sort

정렬해야 하는 데이터(파일)이 [[3, 4], [6, 2], [9, 4], [8, 7], [5, 6], [3, 1], [2], [∅]]이라고 가정해보자. 각 페이지는 최대 2개의 값을 가질 수 있다. 첫번째 페이지는 [3, 4], 두번째 페이지는 [6, 2]라고 해석이 가능하다. 총 8개의 Page로 구성된 파일임을 알 수 있다.

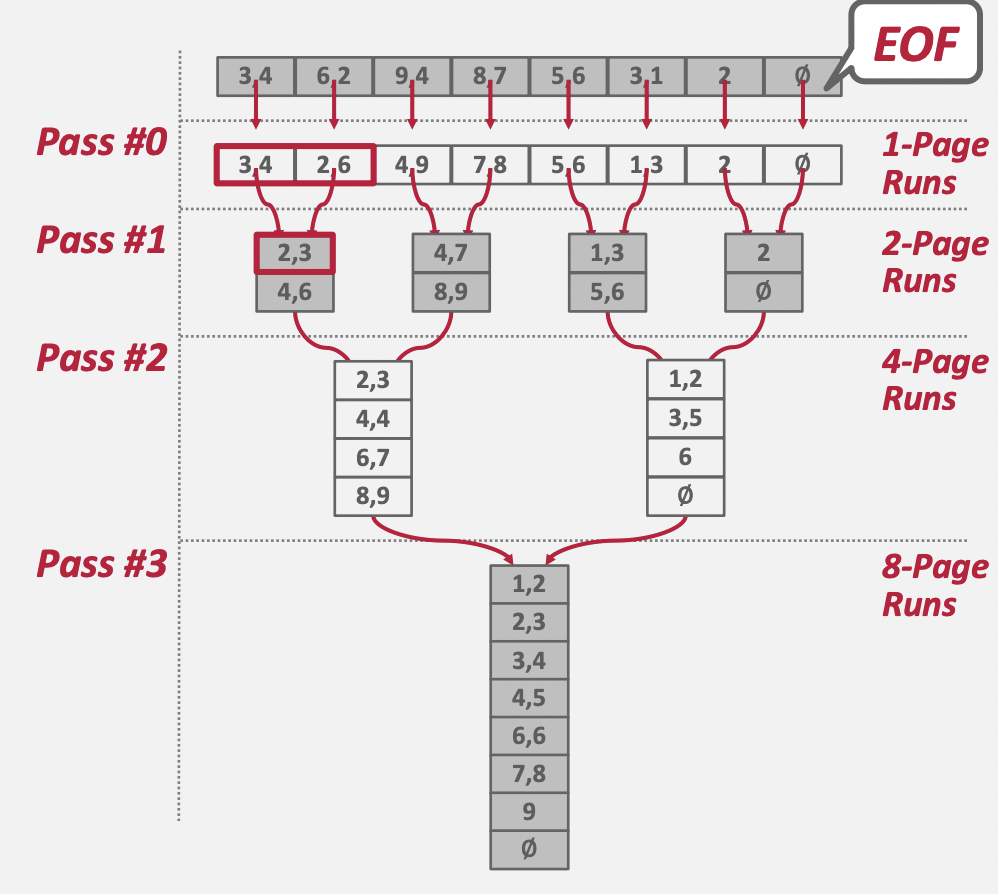
1 PASS

첫 번째 RUN은 1개 Page로 구성된다. 각 RUN 별로 정렬을 수행한 뒤, 결과를 파일로 저장한다. 총 8개의 파일이 생성된다.

• [3, 4]
• [2, 6]
• [4, 9]
• [7, 8]
• [5, 6]
• [1, 3]
• [2]
• [∅]

2 PASS

두 번째 RUN은 2개 Page로 구성된다.

• [[2, 3], [4, 6]] <- [3, 4] + [2, 6]
• [[4, 7], [8, 9]] <- [4, 9] + [7, 8]
• [[1, 3], [5, 6]] <- [5, 6] + [1, 3]
• [[2], [∅]] <- [2] + [∅]

3 PASS

세 번째 RUN은 4개 Page로 구성된다.

• [[2, 3], [4, 4], [6, 7], [8, 9]] <- [[2, 3], [4, 6]] + [[4, 7], [8, 9]]
• [[1, 2], [3, 5], [6], [∅]] <- [[5, 6], [1, 3]] + [[2], [∅]]

4 PASS

네 번째 Run은 8개 Page로 구성된다. 최종적으로 1개의 파일이 생성되었으므로 RUN 반복을 종료한다.

• [[1, 2], [2, 3], [3, 4], [4, 5], [6, 6], [7, 8], [9], [∅]]

중요한 사실은 RUN을 합칠 때 메모리에는 전체 파일을 다 올릴 필요 없이 2개의 페이지(각 입력 파일 별로 1개 씩)만 올라와 있으면 된다는 것이다.

• PASS 수: 1 + ⌈ log2 N ⌉
  • 사실상 Tree의 깊이와 같다.
• Total I/O Cost: 2N * (# of passes)
  • 각 PASS에서 전체 Page를 한번 읽게 되고, 전체 Page를 한번 쓰게 된다.

General External Sort

데이터가 커질 수록 2-Way External Sort는 느려진다. N이 커지며 PASS 수와 Total I/O Cost 모두 증가하기 때문이다. 만일 Merge 단계에서 2개가 아닌 3개, 4개 등 K개의 RUN을 한번에 Merge 하면 PASS수와 Total I/O Cost는 어떻게 변화할까?

• PASS 수: 1 + ⌈ logk N ⌉
  • 기존 2였던 k가 3, 4 등으로 증가하며 트리의 높이가 낮아진다.
  • 결과적으로 PASS 수가 줄어든다.
• Total I/O Cost: 2N * (# of passes)
  • 각 PASS에서 전체 Page를 한번 읽고, 한번 쓰는 것은 변화 없기 때문에 Total I/O Cost 계산식은 변화하지 않는다.

k를 늘리므로써 PASS 수를 줄여 전체 정렬 성능을 높일 수 있다. 단, k개의 Page를 한번에 메모리에 올려야 하기 때문에, 메모리 사용량은 k가 늘어날 수록 비례해서 늘어나게 된다.

정리하자면,

• External Sorting은 모든 데이터를 메모리에 올릴 수 없을 때 사용할 수 있는 정렬 기법을 의미한다.
• External Merge Sort를 사용하면 logN 시간 복잡도로 External Sorting을 구현할 수 있다.
• External Merge Sort의 성능을 올리고 싶다면, 한번에 Merge할 RUN의 수(k)를 늘려주면 된다. 단, Trade-Off로 메모리 공간을 많이 사용하게 된다.

External Sorting은 아니지만 23. Merge k Sorted Lists을 풀어보면 개념 잡기에 도움이 될 것 같다.

Comparison Optimizations

정렬 시 비교 연산을 최적화 하는 기법들을 소개한다.

• Code Specialization: 함수 포인터를 통해 비교 연산 알고리즘을 전달하는 대신, 특정 키 타압에 맞는 비교 연산 알고리즘을 명시적으로 전달하는 방식을 의미한다. C++의 Template Specialization을 예로 들 수 있다.
  • C++의 Virtual Method Call 등에 대한 Overhead를 줄이기 위한 방식으로 이해했다.
  • Java 진영에서는 Jit Compiler가 함수를 잘 Inline 할 수 있도록 하고, Method Dispatching 비용을 줄이기 위해 Reflection 대신 MethodHandle 등을 사용하도록 하면 비슷한 효과가 나오지 않을까? 라는 생각이 든다.
• Suffix Truncation: 긴 길이의 두 문자열을 비교하는 알고리즘은 매우 느리게 동작할 수 밖에 없다. 이를 개선하기 위해 Suffix 비교 후, 필요하다면 전체 비교로 Fallback 할 수 있는 방식을 취하도록 한다.

Aggregations

Aggregation은 1개 이상의 Tuple의 값들을 단일 스칼라 값으로 축소하는 연산이다. DBMS는 Grouping에 사용되는 필드의 값이 같은 Tuple들의 집합을 빠르게 찾아내야 하는데, 이 때 사용 가능한 알고리즘이 Hashing과 Sorting이다.

Sorting Aggregation

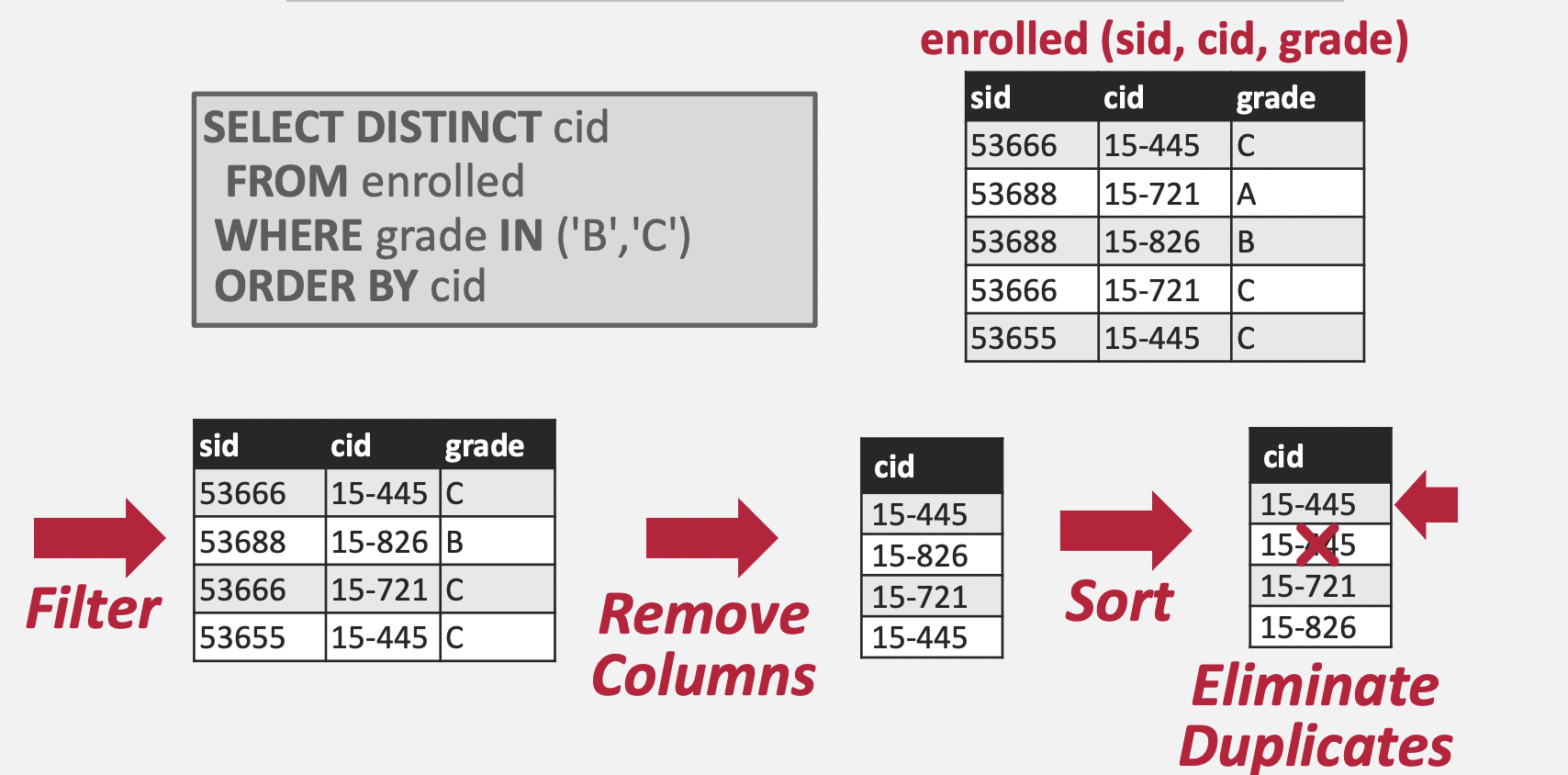
DISTINCT 가 포함된 SQL문을 어떻게 정렬 기반의 알고리즘으로 풀 수 있는지 설명한다. 정렬된 데이터에 대해서는 1 PASS로 유일 값을 찾아낼 수 있다는 것을 생각하면, 위 SQL문도 cid 기준으로 정렬만 한다면 1 PASS로 유일한 cid를 찾을 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public List<Integer> extractDistinct(List<Integer> sortedList) {
  Integer prev = null;
  List<Integer> ret = new ArrayList<>();
          
  // 1 PASS로 유일 값을 추출
  for (Integer val : sortedList) {
    if (prev == null) {
      ret.add(val);
    }
    else if (!Objects.equals(val, prev)) {
      ret.add(val);
    }
    prev = val;
  }

  return ret;
}

Alternatives to Sorting

만일 Aggregation의 결과가 정렬되어 있어야 한다면 Sorting을 사용해야 한다. 그렇지 않은 경우 Hashing을 사용하는 것이 더 적합하다.

예를 들어 앞의 예제의 경우 ORDER BY cid라는 조건이 포함되어 있었기 때문에, Soring으로 접근하는 것이 좋다. 그러나 ORDER BY cid가 없었다면, Hashing으로 접근하는 것이 더 나았을 것이다.(Hashing이 Sorting에 비해 상대적으로 연산 비용이 적으므로)

Hashing

Hashing을 사용하면 Aggregation을 매우 쉽게 구현할 수 있다. 다만 Sorting과 마찬가지로 메모리에 모든 데이터를 올릴 수 없는 경우의 대안이 필요하다.

External Hashing Aggregate

External Hashing Aggregate는 Partition과 ReHash 단계로 이루어지며, 각 단계에서 서로 다른 Hash 함수(Partition - h1, Hash - h2)가 사용된다.

Partition

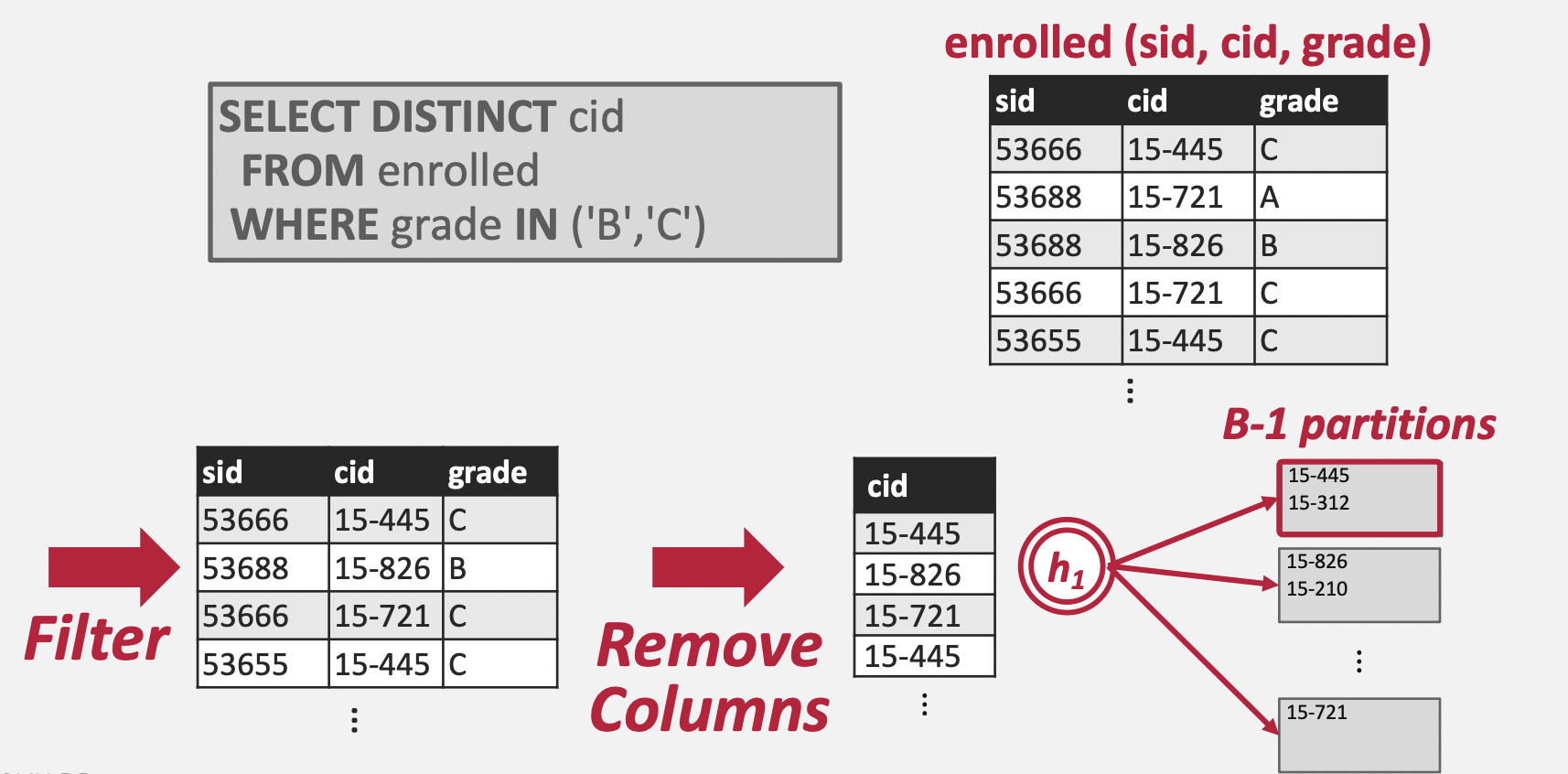
Partition 단계는 N개의 파티션 파일을 생성하는 것으로 시작된다. 이후 각 Tuple의 Key에 Hash Function(h1)을 적용하여 Hash 값을 추출하고, (mod N)을 적용한 뒤 해당 값에 맞는 파티션 파일에 Tuple Key를 쓴다. 이 때 주의해야 할 것은 중복 등을 고려하지 않고 그냥 쓴다는 것이다.

• 디스크에는 총 N개의 파티션 파일이 생성된다.
• 각 파티션 파일에는 Key의 Hash 값이 동일한 Tuple들이 포함되어 있다.
• 각 파티션 파일에는 중복된 Key들이 존재할 수 있다.
• 파티션 파일에는 Page 단위로 데이터를 쓰게 된다.

ReHash

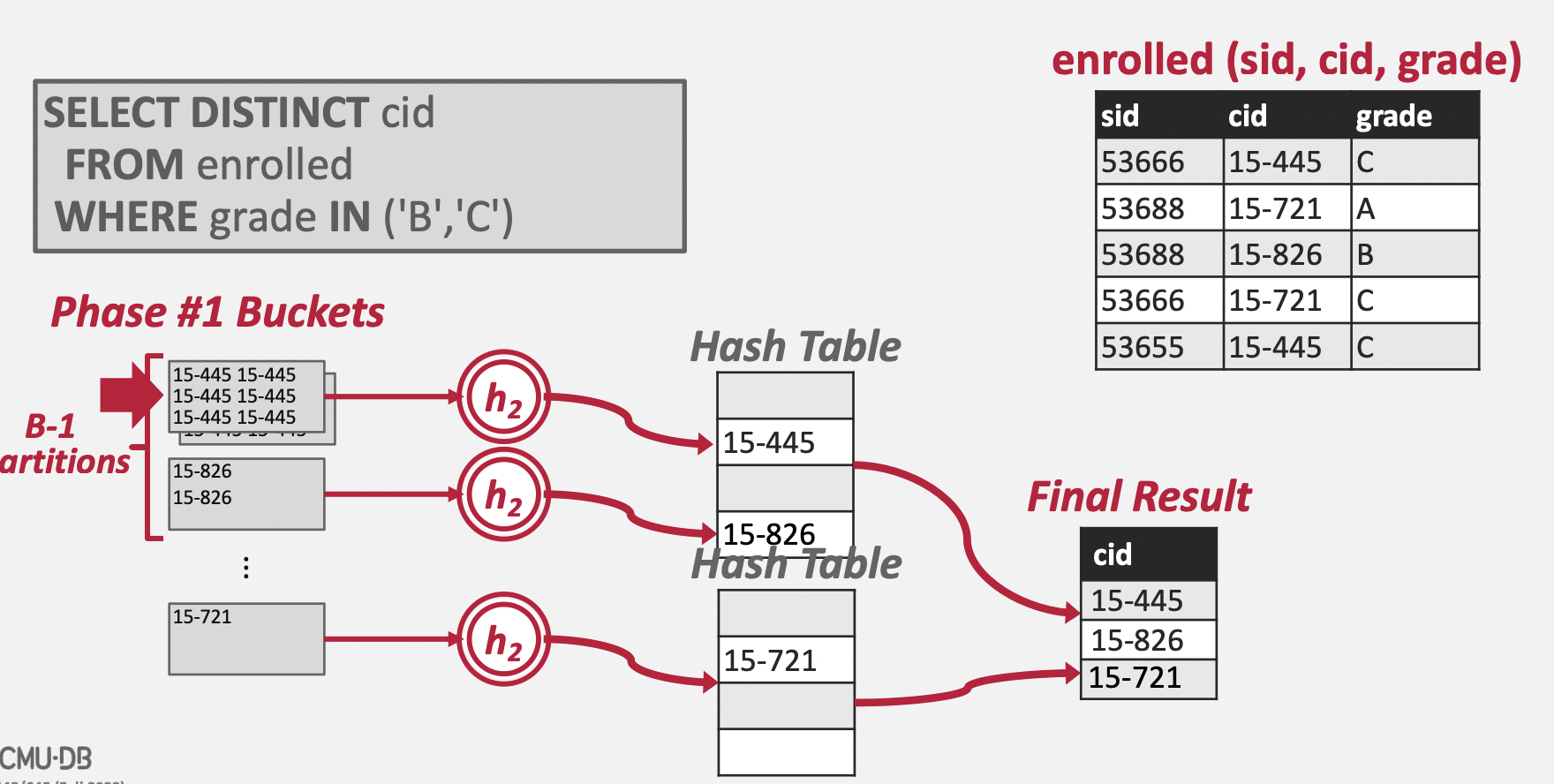
Partition 단계가 끝나면 모든 Key 값들이 파티셔닝되어 디스크에 저장되어 있을 것이다. 디스크에 저장된 Key 값들을 읽어 Hash 테이블을 만들어야 한다. 그 전에 Partition 파일들의 특성에 대해 생각해보자.

• 하나의 파티션 파일 안에는 중복된 Key 값이 존재할 수 있다.
• 서로 다른 파티션 파일들이 같은 Key 값을 포함할 수 없다.

즉, 파티션 단위에서만 중복이 제거되면 모든 파티션을 합쳐도 중복이 발생하지 않는다는 결과를 얻어낼 수 있다. 그래서 파티션 별로 메모리에 Hash Table을 생성하고, 파티션 데이터를 읽어 해당 Hash Table에 채워 넣는다. 이후 모든 Hash Table을 Merge하면 최종 Hash Table을 도출할 수 있게 된다.

Rehash 시 메모리가 부족하다면?

Rehash 과정에서 사용되는 Hash Table의 크기가 메모리 용량을 넘어설 수 있다. 이러한 문제를 해결할 수 있는 방법은 다음과 같다.

1. 파티션 파일이 더 적은 수의 Key를 포함하도록 한다. 즉, 파티션의 개수(N)를 늘린다.
2. Rehash 대상 파티션을 한번 더 파티셔닝하여 처리한다.
3. Rehash에서 Hash Table이 아닌 Sorting을 사용한다.

개인적인 생각

이번 강의에서 나온 정렬, 해시 알고리즘들은 실제로 분산 병렬 애플리케이션에서도 많이 사용된다. 또한 각 알고리즘에서 사용되는 파라메터 값들이 결과적으로 분산 병렬 애플리케이션의 튜닝에도 사용된다.

External Hash Aggregate에서 나온 N(파티션 개수)값은 Spark에서의 파티션 수와 동일한 개념으로 생각할 수 있다. 그렇다면 Spark의 Aggregation 연산에서 일부 파티션으로 데이터가 몰려(Skew) 속도가 느려지거나 OOM 등이 발생하는 경우, 위의 “Rehash 시 메모리가 부족하다면?” 에서 제안한 방법과 같이 파티션의 개수를 늘리는 방법으로 해결할 수 있다.(물론 모든 Skew 문제를 해결할 수 있는 것은 아니지만!)

강의를 들으면 들을 수록 기본이 튼튼하면 상위 개념을 이해하기 쉽다는 생각이 든다.